Sumérgete en el fascinante mundo de las fracciones con nuestros Ejercicios De Fracciones Para Niños De 3 De Primaria, diseñados para que los pequeños exploradores aprendan y disfruten de las matemáticas. ¡Prepárate para una aventura matemática que despertará su curiosidad y fortalecerá sus habilidades!
A través de ejemplos interactivos, explicaciones claras y actividades prácticas, este recurso guiará a los niños a través de los conceptos fundamentales de las fracciones, allanando el camino para su éxito en matemáticas.
Introducción a las fracciones para niños de 3º de primaria
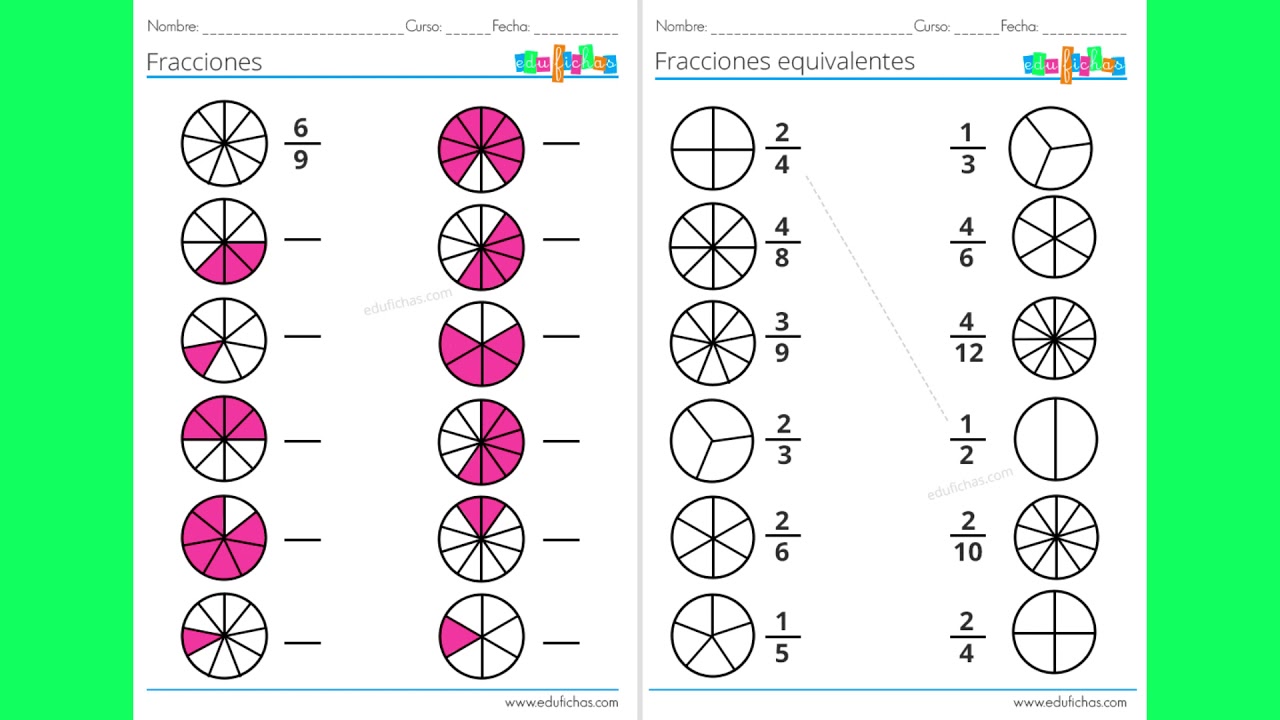
¡Hola, pequeños matemáticos! Hoy vamos a adentrarnos en el fascinante mundo de las fracciones. Son una forma muy útil de representar partes de un todo y nos ayudan a entender mejor el mundo que nos rodea.
Una fracción se compone de dos números: el numerador y el denominador. El numerador indica cuántas partes tenemos, mientras que el denominador indica en cuántas partes se ha dividido el todo.
Cómo se leen y escriben las fracciones
Para leer una fracción, decimos el numerador seguido de “sobre” y luego el denominador. Por ejemplo, la fracción 1/2 se lee como “uno sobre dos”.
Para escribir una fracción, simplemente escribimos el numerador sobre el denominador, separados por una línea horizontal. Por ejemplo, la fracción “uno sobre dos” se escribe como 1/2.
Tipos de fracciones
Las fracciones son una forma de representar partes de un todo. Existen diferentes tipos de fracciones, cada una con sus propias características:
Fracciones propias
Una fracción propia es aquella en la que el numerador (el número superior) es menor que el denominador (el número inferior). Esto significa que la fracción representa una parte menor que el todo.
Ejemplo: 1/2 representa la mitad de un todo.
Fracciones impropias
Una fracción impropia es aquella en la que el numerador es mayor o igual que el denominador. Esto significa que la fracción representa una parte mayor o igual que el todo.
Ejemplo: 3/2 representa más de la mitad de un todo.
Fracciones mixtas, Ejercicios De Fracciones Para Niños De 3 De Primaria
Una fracción mixta es una combinación de un número entero y una fracción propia. El número entero representa el número de partes enteras del todo, y la fracción representa la parte restante.
Ejemplo: 1 1/2 representa un todo y la mitad de otro todo.
Conversión de fracciones impropias a mixtas
Para convertir una fracción impropia en una fracción mixta, sigue estos pasos:
- Divide el numerador por el denominador.
- El cociente es el número entero de la fracción mixta.
- El resto es el numerador de la fracción propia.
- El denominador de la fracción propia es el mismo que el de la fracción impropia.
Ejemplo: Convertir 5/2 a una fracción mixta:
- 5 ÷ 2 = 2 resto 1
- Número entero: 2
- Numerador de la fracción propia: 1
- Denominador de la fracción propia: 2
Por lo tanto, 5/2 es igual a 2 1/2.
Comparación de fracciones
¡Hola, pequeños genios! Hoy nos adentraremos en el fascinante mundo de las fracciones y aprenderemos a compararlas. ¡Prepárense para una aventura matemática llena de diversión y conocimiento!
Comparación de fracciones con el mismo denominador
Cuando las fracciones tienen el mismo denominador, compararlas es muy fácil. Solo tenemos que fijarnos en el numerador. La fracción con el numerador más grande es la más grande.
- Ejemplo: 1/4 es menor que 3/4 porque 1 es menor que 3.
Comparación de fracciones con diferentes denominadores
Cuando las fracciones tienen diferentes denominadores, no podemos compararlas directamente. Primero, necesitamos convertirlas a fracciones equivalentes con el mismo denominador. Podemos hacer esto multiplicando el numerador y el denominador de cada fracción por el mismo número.
- Ejemplo: Para comparar 1/3 y 1/4, podemos convertirlas a fracciones equivalentes con denominador 12:
- 1/3 = 4/12
- 1/4 = 3/12
- Ahora podemos compararlas fácilmente: 4/12 es mayor que 3/12, por lo que 1/3 es mayor que 1/4.
Tabla de comparación de fracciones
Aquí hay una tabla con algunos ejemplos de comparaciones de fracciones:
| Fracción 1 | Fracción 2 | Comparación |
|---|---|---|
| 1/2 | 1/4 | 1/2 es mayor que 1/4 |
| 3/5 | 2/3 | 2/3 es mayor que 3/5 |
| 1/6 | 1/8 | 1/6 es mayor que 1/8 |
Operaciones con fracciones: Ejercicios De Fracciones Para Niños De 3 De Primaria
Las fracciones son una forma de representar partes de un todo. En esta lección, aprenderás a sumar y restar fracciones, una habilidad esencial para resolver problemas matemáticos.
Suma y resta de fracciones con el mismo denominador
Cuando las fracciones tienen el mismo denominador, puedes sumar o restar los numeradores y mantener el denominador. Por ejemplo:
- 1/4 + 2/4 = 3/4
- 3/5 – 1/5 = 2/5
Suma y resta de fracciones con diferentes denominadores
Cuando las fracciones tienen diferentes denominadores, primero debes encontrar un denominador común. El denominador común es el menor número que es múltiplo de todos los denominadores dados.
Pasos para sumar o restar fracciones con diferentes denominadores:
- Encuentra el denominador común.
- Convierte cada fracción a una fracción equivalente con el denominador común.
- Suma o resta los numeradores de las fracciones equivalentes.
- Mantén el denominador común.
Por ejemplo:
- 1/2 + 1/3
- Denominador común: 6
- 1/2 = 3/6
- 1/3 = 2/6
- 3/6 + 2/6 = 5/6
Aplicaciones de las fracciones en la vida real
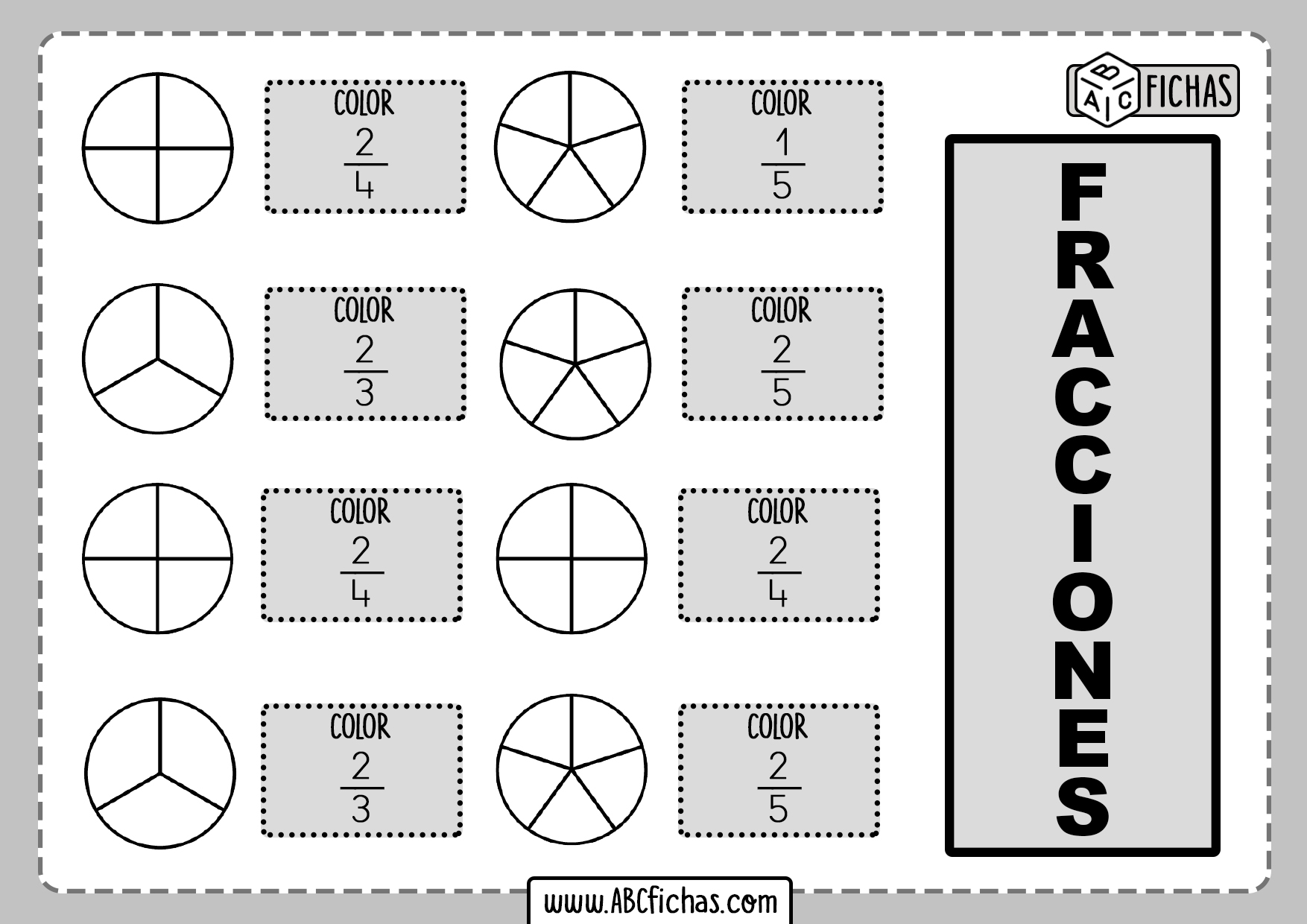
Las fracciones no son solo números abstractos en un libro de texto; son herramientas esenciales que usamos todos los días para resolver problemas del mundo real. Desde repartir pizza hasta medir ingredientes, las fracciones nos ayudan a comprender y manipular las cantidades de forma precisa.
En la cocina
Las fracciones son imprescindibles en la cocina. Cuando sigues una receta, a menudo te piden que uses una fracción de un ingrediente, como 1/2 taza de harina o 1/4 cucharadita de sal. Las fracciones te permiten medir con precisión las cantidades para que tus platos salgan perfectos.
En las compras
Las fracciones también son útiles cuando compras. Si ves una oferta de “3 por 2”, significa que puedes comprar 3 artículos por el precio de 2. Las fracciones te ayudan a comparar ofertas y tomar decisiones informadas sobre tus compras.
En la construcción
Las fracciones son esenciales en la construcción. Los arquitectos y constructores utilizan fracciones para diseñar y construir estructuras, como casas y puentes. Las fracciones les permiten medir con precisión las distancias y los ángulos para garantizar que las estructuras sean seguras y estables.
En la ciencia
Las fracciones también se utilizan ampliamente en la ciencia. Los científicos utilizan fracciones para medir cantidades muy pequeñas, como la concentración de una solución o la masa de un átomo. Las fracciones les permiten recopilar datos precisos y realizar experimentos con éxito.
¡Con Ejercicios De Fracciones Para Niños De 3 De Primaria, las fracciones se convierten en un juego de niños! Proporcionando una base sólida en este concepto esencial, empoderamos a los niños para resolver problemas, pensar críticamente y desarrollar una comprensión profunda de las matemáticas.
¡Anímalos a explorar, descubrir y conquistar el mundo de las fracciones con confianza y entusiasmo!
FAQ Resource
¿Qué son las fracciones?
Las fracciones son una forma de representar partes de un todo. Se escriben como dos números separados por una barra: el numerador (arriba) indica cuántas partes tenemos y el denominador (abajo) indica en cuántas partes se divide el todo.
¿Cómo se leen las fracciones?
Para leer una fracción, decimos el numerador y luego la palabra “sobre” seguida del denominador. Por ejemplo, 1/2 se lee como “uno sobre dos”.
¿Cómo se comparan las fracciones?
Para comparar fracciones con el mismo denominador, simplemente comparamos los numeradores. La fracción con el numerador más grande es mayor. Para comparar fracciones con diferentes denominadores, primero debemos encontrar un denominador común.
